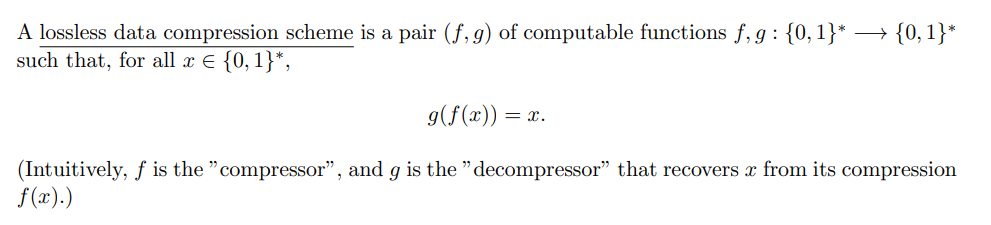(Solved): Question: Prove: For every lossless data compression scheme (f, g) and every n N, there is ...

Question: Prove: For every lossless data compression scheme (f, g) and every n ? N, there is a string x ? {0, 1} ⁿ such that |f(x)| ? |x|.

 

Note: {0, 1} ⁿ  is the set of strings n

|x| = the length of string x

and  |f(x)| = length of compression

Use the concept of Number theory and Kolmogorov complexity to answer this.

A lossless data compression scheme is a pair (f,g) of computable functions f,g: {0,1}* + {0,1}* such that, for all x € {0,1}*, g(f(x)) = = ? . (Intuitively, f is the "compressor”, and g is the "decompressor” that recovers x from its compression f(x).)