Expert Answers

F(a,b,c,d) =?m(3,7,8,11,12,14,15)

15. Show that - (p-1)!= p - 1 mod p?p - 1)/2.

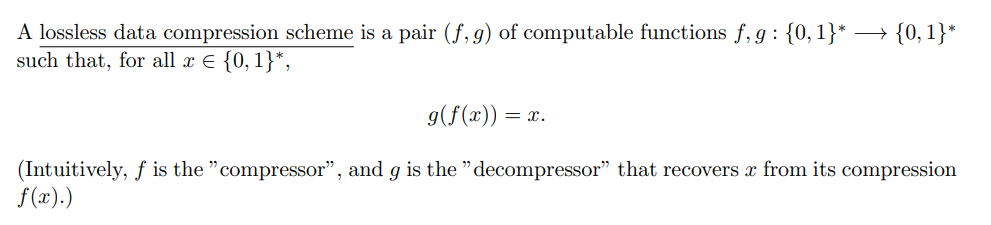
Question: Prove: For every lossless data compression scheme (f, g) and every n ? N, there is a string x ? {0, 1} ⁿ such that |f(x)| ? |x|.

 

Note: {0, 1} ⁿ  is the set of strings n

|x| = the length of string x

and  |f(x)| = length of compression

Use the concept of Number theory and Kolmogorov complexity to answer this.

A lossless data compression scheme is a pair (f,g) of computable functions f,g: {0,1}* + {0,1}* such that, for all x € {0,1}*, g(f(x)) = = ? . (Intuitively, f is the "compressor”, and g is the "decompressor” that recovers x from its compression f(x).)

Assume that you are the owner of a solar panel shop. Owing t o the ongoing power crisis in your area and sharp increases in electricity prices over the last few years, there is a growing demand for alternative electricity in the form of solar panels. you sell and install these panels. you are making use of an electrician (the other product) to activate these panels for your customers. you are operating in a perfectly competitive market. the demand curve for your panels (in rand) is as follows: Qd=2000 - P+0.08Y+6P2

Thank you for helping me. 

- . By Green's formula , let A - ( M (2,4), N(X,Y),0). Also, = n suppose that a single closed curve C is represented as =(((t), y(t),0) Castsb). In this case, show that the Green's formula can be written as dr , ( S.A.dk - SS. COXA) E dado R C

Q1; What are the Major risk-control techniques ?

 

Q2 ; Shortly explain the PRINCIPLE OF INSURABLE INTEREST?

Question no. 4 out of 20 Answer this question Use the backward-difference formula to approximate f'(0.6) for the table data points given that h = 0.03. Select the correct answer 387.3171 B 497.9791 ?? 0.5400 0.5700 0.6000 0.6300 0.6600 ?? 17.4230 20.3251 23.6450 27.4383 31.7680 C 442.6481 D 77.4634 E 110.662

 

To ports Internet Censorship Suppliers Insourcing Quality of work life Age Job creation through foreign direct investment O The deliberate blockage and denial of public access to information posted on the internet O ? O O O Providers of inputs. O O Is the overall quality of human experiences in the workplace. O O ? One of the aspects of demographics O O O

Quality Management Course 

Problem 1 1- The failure rate of the milling and grinding machines are 0.0003 and 0.0002 failure/hour, respectively. The probability that any Turning Machine will fail immediately after 50 hours given that it does not fail until 50 hours is 0.0035. Calculate the probability that the system will fail at any point during the 50 hours of work. Note that the failure rate of the machines is constant. Milling Machine Turning Machine Turning Machine OBS Turning Machine Grinding Machine

Solve #10 according to the hint below:

9. Suppose that A is a nonempty set, and f is a function that has A as its domain. Let R be the relation on A consisting of all ordered pairs (x, y) such that f(x) = f(y). a) Show that R is an equivalence relation on A. b) What are the equivalence classes of R? 10. Suppose that A is a nonempty set and R is an equivalence relation on A. Show that there is a function f with A as its domain such that (x, y) E R if and only if f(x) = f(y). = Although the situation in Exer 9 is not exactly the same as here, be sure to do that exercise first to warm-up. (In Exer 9 the function f is given 1st, and then a relation R is to be defined in terms of f. Here the relation R is given 1st, and then a function f is to be defined in terms of R.) Here no codomain B is being given, but to solve the problem you will need to specify a particular set B. Outline for creating an f that works: Choose the codomain B for f to be P(A), the power set of A. Then you need to specify a particular rule to define a function f that assigns a particular subset of A to each element of A. (You'll need to refer to R, of course.) To prove that your f has the required property, consider Theorem 9.5.1. THEOREM 1 Let R be an equivalence relation on a set A. These statements for elements a and b of A are equivalent: (i) arb (ii) [a] = [b] (iii) [a] n [b] 0