EXAMPLE 5 A man walks along a straight path at a speed of 2(m)/(s). A searchlight is located on the ground 8 m from the path and is kept focused on the man. At what rate is the searchlight rotating when the man is 6 m from the point on the path closest to the searchlight? SOLUTION We draw the figure to the left and let x be the distance from the ma

Question

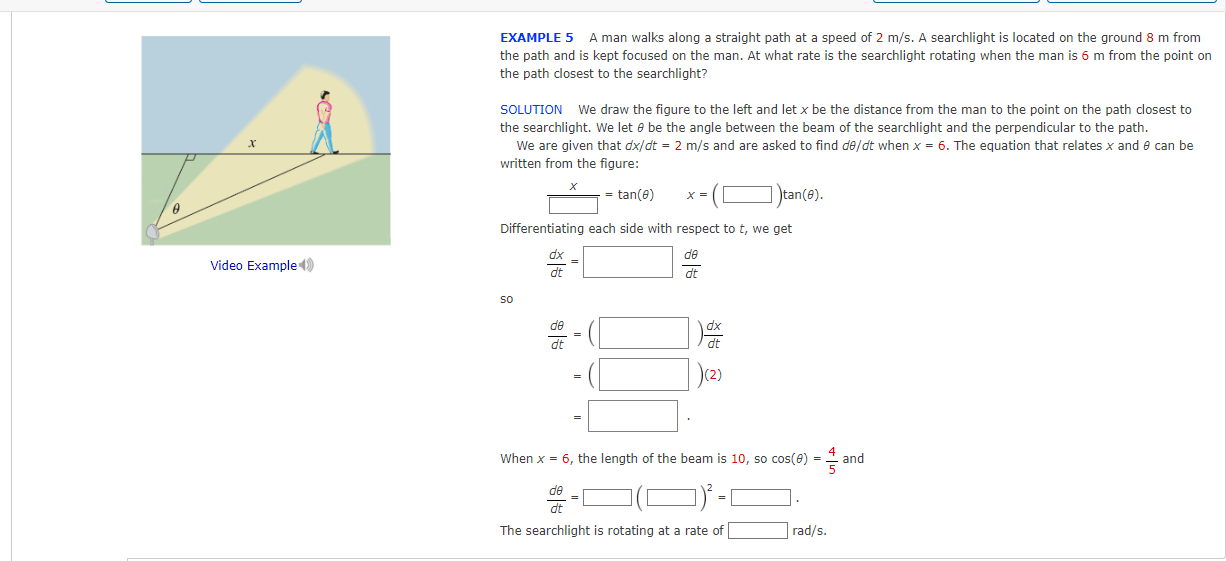
EXAMPLE 5 A man walks along a straight path at a speed of

2(m)/(s)

. A searchlight is located on the ground 8 m from the path and is kept focused on the man. At what rate is the searchlight rotating when the man is 6 m from the point on the path closest to the searchlight? SOLUTION We draw the figure to the left and let

x

be the distance from the man to the point on the path closest to the searchlight. We let

\theta

be the angle between the beam of the searchlight and the perpendicular to the path. We are given that

d(x)/(d)t=2(m)/(s)

and are asked to find

d(\theta )/(d)t

when

x=6

. The equation that relates

x

and

\theta

can be written from the figure:

x,=tan(\theta ),x=(,)tan(\theta )

Differentiating each side with respect to

t

, we get When

x=6

, the length of the beam is 10 , so

cos(\theta )=(4)/(5)

and

(d\theta )/(dt)=,(,)^(2)=

The searchlight is rotating at a rate of

ra(d)/(s)

.

student submitted image, transcription available below

Accepted Answer

Expert Answer to - EXAMPLE 5 A man walks along a straight path at a speed of 2(m)/(s). A searchlight is located on the

Answer

Solution for - EXAMPLE 5 A man walks along a straight path at a speed of 2(m)/(s). A searchlight is located on the

Answer

This an additional answer to - EXAMPLE 5 A man walks along a straight path at a speed of 2(m)/(s). A searchlight is located on the

(Solved): EXAMPLE 5 A man walks along a straight path at a speed of 2(m)/(s). A searchlight is located on the ...

View Expert Answer

Expert Answer

Buy This Answer $5

Place Order